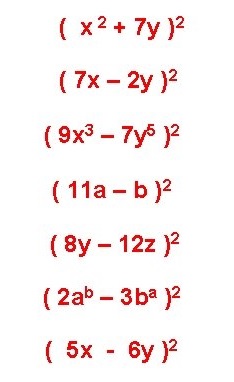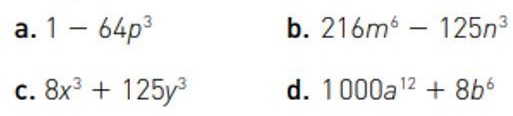Objetivo: Desarollar el producto notable de una suma por su diferencia.
El producto de una suma por su diferencia es de la forma (a+b)(a-b) donde a+b es la suma de 2 términos y a-b es la diferencia de esos términos.a=4m5
|
MATEMATICA 10 EGB
2021 - 2022
EJERCICIOS
Resuelva los siguientes ejercicios en su cuaderno de MATEMÁTICAS.
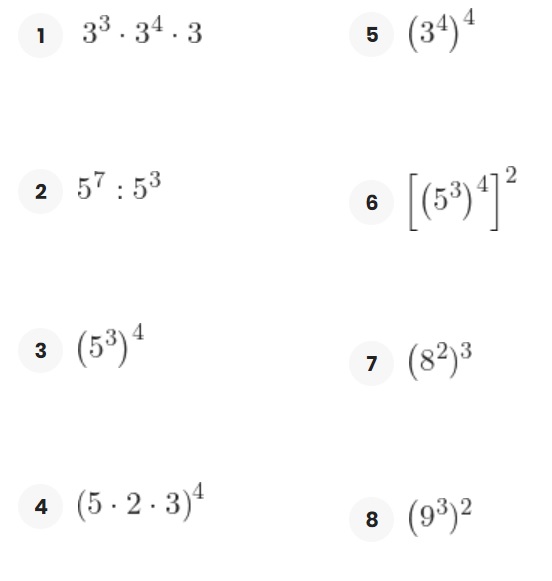
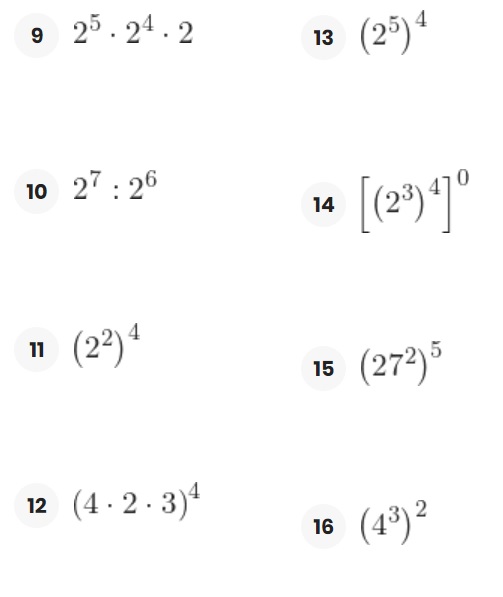
En el espacio adjunto suba una fotografía de sus ejercicios.
Binomio al cubo
¿Qué es un binomio al cubo?
Los binomios al cubo, también conocido como cubo de un binomio, pertenece a los productos notables, de hecho es una de sus muchas identidades. Los productos notables contienen fórmulas que son de mucha importancia en el desarrollo y resolución de algunos procedimientos matemáticos.


Calculadora
Pizarra
ACTIVIDAD N 1
svasquez_17@live.com
liveworksheets.com
ACTIVIDAD N 2
Resuelva en su cuaderno los siguientes binomios.
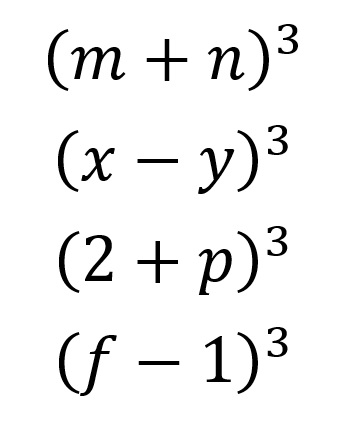
Suma por la Diferencia

|
Matemática > Segundo Año >
Producto notable de una suma por su diferencia |
Proyecto Interdisciplinario
Portafolio estudiantil

FACTORIZACIÓN
Factor común
Se dice que un polinomio tiene factor común cuando una misma cantidad, ya sea número o letra, se encuentra en todos los términos del polinomio.
Si en todos los términos de un polinomio figura un factor común, dicho polinomio es igual al producto de ese factor por el polinomio que resulta al dividir cada término por ese factor.
Ejemplos:

Actividad N1. Ejercicios interactivos.
Correo para el envío de la actividad: svasquez_17@live.com
liveworksheets.com
Actividad N2. Ejercicios prácticos.
Resuelva los siguientes ejercicios.
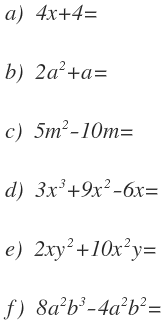
PROYECTO
Descargue el archivo adjunto.
Diferencia de Cuadrados
Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.

Ejemplos

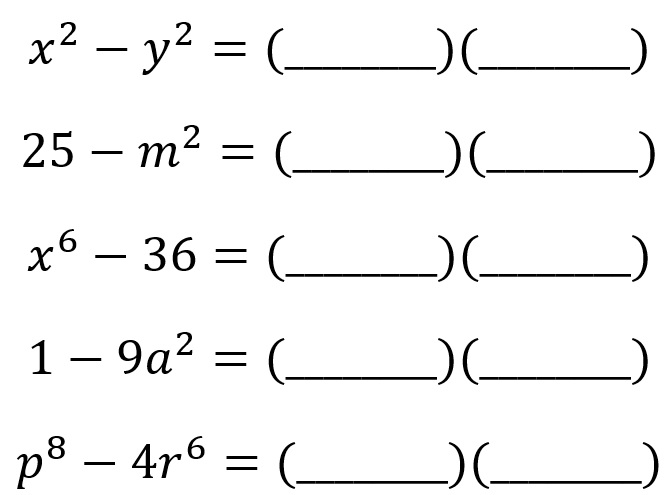
ACTIVIDADES
liveworksheets.com
Resuelva los siguientes ejercicios en su cuaderno.
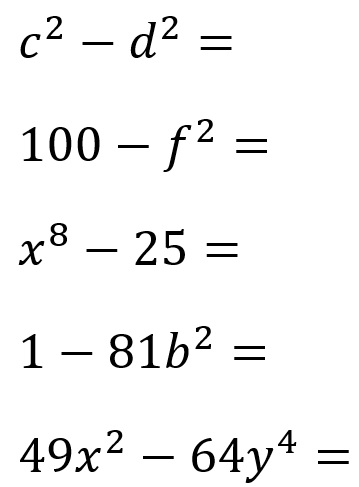
Suma o Diferencia de Cubos